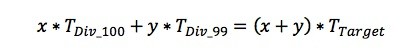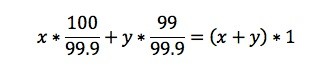RTC設計で重要な温度補償、有効な手段を検討する：RTC設計講座【後編】（3/3 ページ）

[Gordon Lee，EDN]

MEMS共振器内蔵RTC

　TCXO内蔵RTCは完璧なソリューションのようにみえる。しかしながら、これにも依然としていくつかの弱点がある。32.768kHz水晶発振器を搭載したRTCはウェアラブルや他の小型アプリケーションには分厚すぎるのだ。水晶振動子のサイズを決めるのは周波数であるから、サプライヤーが水晶振動子のサイズを小さくすることはできない。サイズをさらに小さくするには、異なるタイプの共振器を使用すればいい――それがMEMS共振器内蔵RTCである。

　MEMSとは微小電気機械デバイスのことで、振動して非常に安定した基準周波数を生成する。最新世代のMEMSは水晶振動子よりもはるかに温度変化の影響を受けにくい。その質量は水晶振動子の数千分の一だ。また、MEMS共振器の重量ははるかに少ないため、振動や機械的衝撃にも比較的強い。MEMS共振器はICダイにマウントされるため、パッケージサイズもほぼダイサイズと同じくらい小さくできる。

　MEMS共振器は、一般に水晶共振器よりも多くの電力を消費する。設計者は消費電流が少なくなるようMEMS共振器のインピーダンスを最大化することで消費電力を抑えられる。等価インピーダンスは次の式から求められる。

　インピーダンスはC_Lが0に近づいたときに最大となる。この例では、共振器はその並列共振周波数付近で動作する。これにより、消費電流と消費電力が低減する。ただし、負荷コンデンサーによって温度補償のための共振周波数調整を行うことはできない。単純に、負荷コンデンサーが存在しないからだ。

　共振器の出力周波数は負荷容量を増減しても変えられないため、設計者は周波数をRTC計時ロジックへの供給前に調整する別の方法を実装する必要がある。共振器出力とRTC計時ロジック入力の間に分周器を挿入するのも一つの方法だ。

分数分周器

　デジタル設計の入門クラスでは、任意の正の整数で割ることができるクロック分周器の実装方法をいくつも学ぶだろう。分数分周器は任意の分数でクロックを分周できる。分数分周器の仕組みを理解するために、ここではごく単純な例について考えてみよう。入力クロックを100Hzと仮定し、100Hzリファレンスクロックから1Hz出力を得るときは、単純にクロックを100で割ることができる。

図2：単純なクロック分周器は、0.999Hzから1.009Hzの間にある厳密な出力周波数を生成できない［クリックで拡大］ 出所：Analog Devices

　もしリファレンス入力クロックを100Hzから99.9Hzに変えたとしたら？　99.9Hzから1Hzを生成するにはどうすればいいのだろうか。除数が100なら、出力は0.999Hzになり、1Hzにはわずかに届かない。除数が99なら出力は1.009Hzとなり、1Hzを若干超える。図3は、1/100分周と1/99分周のクロック出力信号の重なり部分と、1Hzクロックの理想的な立ち上がりエッジがグレー領域内のどこかにあることを示している。

図3：1/99分周の出力クロックと1/100分周の出力クロックを示している［クリックで拡大］ 出所：Analog Devices

　単純なクロック分周器は、0.999Hzから1.009Hzの間にある厳密な出力周波数を生成することができない。分数分周器には、除数を調節する制御回路があるため、その出力クロック周波数を0.999Hzと1.009Hzの間で切り替えられる。2つの除数の出現率が注意深く設計されていれば、分周器は理論的にはいずれ0.999Hzから1.009Hzの間の平均周波数を生成できるようになる。各クロックサイクルは厳密な1Hzクロックサイクルではないものの、時間の経過とともに得られる平均出力クロックはかなり正確になる。

　0.999Hzクロックの出現数をx、1.009Hzクロックの出現数をyとしよう。x対yの正確な出現率を計算するには、次のような式を立てられる。

　上記において

• xは、1/100分周クロックサイクルの出現数
• yは、1/99分周クロックサイクルの出現数
• T_{Div_100}は、1/100分周の1クロックサイクルの周期（この例ではT_{Div_100}＝100/99.9）
• T_{Div_99}は、1/99分周の1クロックサイクルの周期（この例ではT_{Div_99}＝99/99.9）
• T_Targetは、ターゲットとする1平均クロックサイクルの周期（この例ではT_Target＝1）

　をそれぞれ表す。

　全ての周期変数を代入すると、次のようになる。

　この式でいくつか代数操作を行った後のx:yの比は9:1となる。つまり、分数分周器の入力クロックが99.9Hzであるときは、1/100分周のクロック数が9クロックになる毎に1/99分周のクロックを1つ挿入する。合計で10クロックサイクルを越えると、平均周波数がきっかり1Hzになるだろう。この9:1のパターンは、入力周波数が変わるまで繰り返し継続される。前述の通り、入力周波数は温度-周波数変換関数または較正から得られる参照テーブルによって決定できる。

原文へのリンク