2つの式の導出(2)―― Cの定義:たった2つの式で始めるDC/DCコンバーターの設計(2)(1/4 ページ)
今回はテーマとした「2つの式」のなかで前回説明しきれなかったキャパシターの式について説明したいと思います。キャパシターは電子回路で抵抗器、インダクターと並んで多用される電子部品です。
前回はインダクタンスの定義、法則、公理を考えました。定義、法則、公理は理論の前提条件となる理(ことわり)ですがこれらの理から導かれる諸式に基づいてインダクターの電流が瞬時には変化しにくいこと、強引に急峻に電流を遮断するとスパイク電圧と呼ばれる誘起電圧が発生することについて説明しました。
前回のこの誘起電圧発生の説明文中で電流遮断部をスイッチのようにイメージできる説明をしてしまいましたが、正しくは、電流遮断部はインダクタンス中に直列に分布定数的に存在します。この見かけの集合体が等価抵抗Rです。
今回はテーマとした「2つの式」のなかで前回説明しきれなかったキャパシターの式について説明したいと思います。キャパシターは電子回路で抵抗器、インダクターと並んで多用される電子部品です。
キャパシタンスに関する式
キャパシタンスについてもインダクタンスと同様に、最初に容量Cの定義を考えます。
キャパシタンスの定義には次に説明する2つの方法がありますが結果は同じになります。
[1. 点状電荷による定義]
図1に示すように、『電気的に孤立(浮遊)した点状電荷Qを考え、無限遠を基準とした電荷Qの電位がVである時の電荷Qと電位Vとの比』 をキャパシタンス(静電容量)Cと呼び、式で表せば1式になります。
ただし、この定義方法は無限遠が必要なので精度の確保が困難なことや再現性の難しさから次の並行平板電極の定義が主として用いられています。
[2. 並行平板による定義]
図2に示すように、『2つの並行平板電極の電荷がそれぞれに+Q、−Q*である時、電荷Qと電極間電位差Vとの比』をキャパシタンス(静電容量)Cと呼び、式で表せば同じく1式になります。
*『孤立系における電荷(電気量)の総量は恒久に変わらない』という電荷保存則に従って一方の電極に電荷+Qを与えると対向電極には−Qの電荷が誘起されます。
図2では各電極板の両面に1/2ずつ電界は生成されます。つまり+極板では両面から1/2ずつ無限遠に向かって放出され、対向する−極板では同様に両面から1/2ずつ吸収されます。
キャパシターを含む全空間を考えると2枚の電極内の空間では
(+1/2)−(−1/2)=1の電界になり、電極の外部空間では(+1/2)+(−1/2)=0ですから電界は電極内部にしか存在しません。
SI単位系ではQ=I×sと定義されています。したがってこの両辺を時間で微分すれば電流Iを表す式として2式を得ることができます。文献によってはQ=I×sをC(クーロン)=A(アンペア)×sと表記している文献もありますが本稿ではCを容量(Capacity)の表記に、またAを面積(Area)の表記に使用していますので電荷をQ、電流をIと表記します。
インダクタンスの場合と同様に1式を時間で微分し、2式を代入します。
さらに3式を微少時間Δtで近似し、移項すると4式を得ます。
4式も設計に頻繁に使用します。以後3式、4式をCの式と呼ぶことにします。またキャパシタンスの性質を持つ素子をキャパシターと呼びます。
Copyright © ITmedia, Inc. All Rights Reserved.


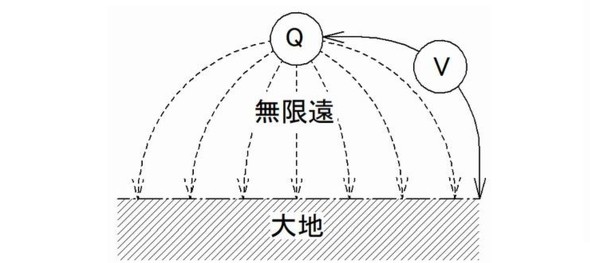 図1:点状電荷によるキャパシタンスの定義
図1:点状電荷によるキャパシタンスの定義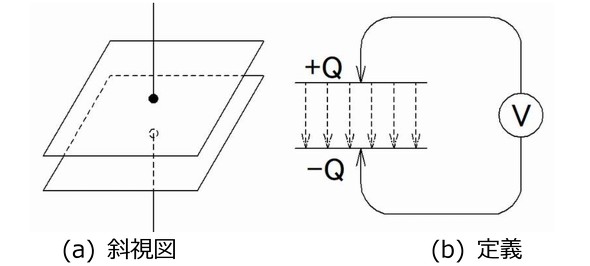 図2:並行電極によるキャパシタンスの定義
図2:並行電極によるキャパシタンスの定義





