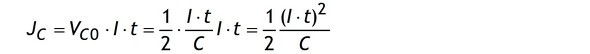2つの式の導出（2）―― Cの定義：たった2つの式で始めるDC/DCコンバーターの設計（2）（2/4 ページ）

[加藤博二（Sifoen），EDN Japan]

キャパシターに蓄積されるエネルギーJ_C

図3：キャパシターへのエネルギー転移［クリックで拡大］

　キャパシターを直接電圧源に接続すると3式でdt＝0としたことになり、dVの値に関わらず無限大の電流が流れて計算ができません。
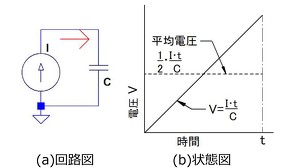
　ここでは急激な電流変化が起きないように図3に示すように定電流源IでキャパシターCを充電することを考えます。

インダクタンスの場合と同様に、電流源Iからのエネルギー変化だけを考えるために時刻0においてキャパシタンスの電圧は0とします。また時刻tはt＝0＋Δtです。

　この時、キャパシターの電圧VはCの式（ΔV＝(I/V)･Δt）に従い時間とともに変化します。このことは電流源IからV×I×ΔtのエネルギーJ_Cが供給されることを意味します。
　時刻tにおいてキャパシターCには

の電圧が充電されていますがこの期間の三角波電圧の平均値V_C0は

です。したがって時刻tまでに電流源Iから出ていったエネルギーJ_Cは電圧×電流×時間ですから、

ですがCの式（t･I＝V･C）を代入するとJ_Cの式として時間に依存しない

が得られ、現在の電圧値Vが分かればエネルギーJ_Cを計算することができます。
　図3の回路では損失になる素子がありませんので電流源Iから出ていったエネルギーJ_CはキャパシタンスCに蓄積されることになります（エネルギー保存則）。
　5式はリップル電圧や動作保持時間の計算などに使用されます。

　既に説明したように3式で行っている微分とは変化量dVと変化量dtの比率です。したがって分母が0では計算ができないことは自明です。

［電圧連続性］
　Cの式（ΔV＝(1/C)･Δt）からΔt≅0であるならばΔV≃0と見なすことができます。つまりキャパシタンスの電圧は瞬時には変化しません。この性質をキャパシタンスの疑似定電圧性と呼びます。
　5式の蓄積エネルギーJ_Cには時間項がありませんので図3の電流が遮断されても変化しません。したがってインダクタンスと同様に「エネルギー保存則」に従って電圧Vは同じ極性を維持し続けることになります。この性質をキャパシタンスの電圧持続性と呼びます^＊。

　ここで説明したようにキャパシターには疑似定電圧性と呼ばれる、瞬時には電圧が変化しない特性がありますのでスイッチなどで急激に電荷を放電すると過大な電流、極言すれば無限大の電流が流れる可能性もあります。
　この過大な電流はスイッチング電源などでは周辺素子に損傷を与える要因になります。また急峻な電流変化は電磁波として空間や機器内を伝搬し電磁波ノイズとして規制の対象になります。

＊電圧の極性が瞬時に反転しても形式上はエネルギー保存則を満せますがCの式（I＝C(dV/dt)）に従って無限大の電流が流れますのでエネルギーが放出され保存則を満たせません。

　これで今回のシリーズで使用する2つの式がそろいました。電気に関する法則や図式解法を除いてこの2つの式を使ってできる限りDC/DCコンバーターの設計を進めていきます。