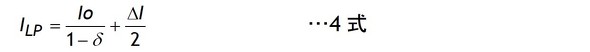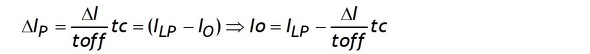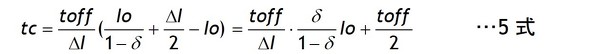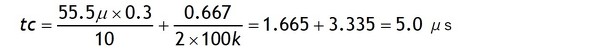ステップアップ形DC/DCコンバーターの設計(6)チョーク電流連続時の充電モード:たった2つの式で始めるDC/DCコンバーターの設計(13)(3/4 ページ)
» 2025年01月21日 11時00分 公開
[加藤博二(Sifoen),EDN Japan]
モードIIの各部電流波形
図2から分かるように放電電荷の波形が五角形なので放電電荷の面積(=Q)を計算で求めると式が複雑になります。ここではキャパシターの充電波形からリップル電圧を求めます(定常状態では充電電荷=放電電荷です)。
電流連続モードですからチョーク電流ILはtoff期間中に2式のΔIだけ変動します。
したがってチョーク電流の最大値ILPは平均ILにΔIの1/2を加えた4式になります。
このILPからターンオフと同時に
の傾きでILは変化し、時刻tcでILがIoに達すると同時にキャパシターへの充電が終わります。この時のチョーク電流の変化幅ΔIpは(ILP−Io)です。
ΔIとΔIpは比例関係(ΔI/toff=ΔIp/tc)ですからΔIpは次の式に置き換えができます。
この式にILPを表わす4式を代入すると次式が得られます。
この式をtcについて解くと5式が得られます。
この5式に
を代入すると6式が得られます。
【計算例】
6式にL=55.5uH、Io=0.3A、Vcc=10V、δ=0.333、f=100kを代入すると
となり図1(b)の値とほぼ一致します。
またIo=0.6Aの時、tc=6.67μs(=toff)になりモードI、IIの臨界になります。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentPR
Pickup ContentsPR
記事ランキング
Special SitePR
あなたにおすすめの記事PR
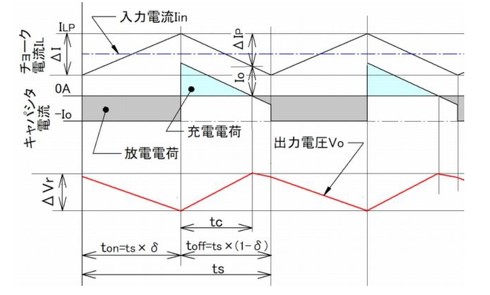 図2:モードIIの電圧・電流
図2:モードIIの電圧・電流