フェライト（5） ―― 磁気回路の基本式：中堅技術者に贈る電子部品“徹底”活用講座（5）（2/2 ページ）

[加藤博二（Sifoen），EDN Japan]

磁気回路に必要なパラメータ

コア寸法

　SI単位系の次の記号でコアを表すことにします。また、全体の漏洩（ろうえい）磁束やギャップ部分の漏洩磁束についてはここでは考慮せず、理論式を考えることにします。

断面積：Ae　　磁路長：l　　巻回数：N　　磁束密度：B＝φ/Ae　　電流：I　　磁束：φ　　インダクタンス：L
真空中の透磁率：μ₀＝4π×10⁻⁷　　比透磁率:μ_S　［μ=μ₀×μ_S］

起磁力（磁界の強さ）

　起磁力をFとした場合に、F＝N×I［A］と定義し、単位長さ当たりの起磁力を“磁界の強さH”と呼び、H＝F/l＝(N×I/l)［A/m］です（巻回数Nは無次元数のため単位には現れません）。

磁束密度

　磁束密度B^＊3）はその定義からB＝μ･H＝μ［(N×I)/l］です。

＊3）Bmは磁界の強さの最大値Hm_(0-P)に対応する最大磁束密度_（0-P）です。

透磁率

　コアに作用する実際の透磁率μはμ＝μ₀×μ_Sです（μ＝B/H）。

比透磁率

　比透磁率μ_Sは強磁性体などでは200〜1万程度、トランス用フェライトでは1500〜3000程度です。

コアの計算式

　磁路長200mm以下の小型コアの各値を計算する基本的な式を表1に示します。ここでキーになるポイントは磁路長lとエアギャップ長lgの大小関係および、コアの比透磁率μ_Sです。

　下記の表1では小型のコアとして次の仮定をしています。
l＜150mm、lg≪l、μ_S＞1500 これより、l−lg≒l、l/μ_S＝150/1500＝0.1mm≪lg
　つまり、エアギャップ長lgが0.1mmを大きく超えるギャップ付きコアではコアの磁路長lは無視できると仮定しています。

表1：小型コアの近似計算式
注：表1の計算ではコア全体に均一に巻線されていると仮定していますが実際の測定では集中コイル形です。実際、測定コイルの形状や巻回数を変更すると測定値に差が生じますので、できる限り測定条件を固定してください。
　N･I_satはBmsをいくつにするかで異なります。カタログ値の多くはμ_Sの△20％点で定義し、0.37T（テスラ）程度です。実際にはテストコイルのL値が△10％〜△20％減少するDC重畳電流値I_satからN×I_satで求めます。

図1：FEER35Aコアのギャップ特性
太線：実測値　破線：近似値

　表1から小型のギャップ付きコアでは AL∝(Ae/lg)、N･I_sat∝(Bms×lg)という結果が得られます。
　つまり、ギャップ付きコアでは同じ幾何形状（同じlg、Ae、形状）であればインダクション係数ALはケイ素鋼板とフェライトで同じ値が得られることになります。

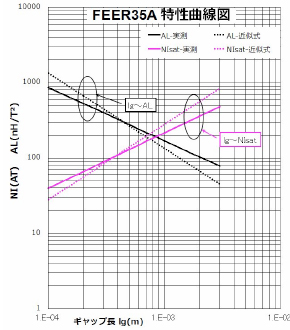
　この近似式の精度を確認するために、図1にTDKのPC47EER35Zのカタログ資料から作成したAL特性、N･Isat特性の実測式と近似式の比較曲線を示しますが両曲線とも傾きに若干の差はあるものの、同傾向を示していることが分かります。これらの特性曲線はギャップ特性とも呼ばれます。

　また、TDKのPC47材の3種類のコアで計算した結果を表2に記します。

　lg＝0.3mmの条件ではN･I_satの実測値は、
　　75.4AT （EER25.5）
　　70.9AT （EI35）
　　88.7AT （EER35Z）
であり、形状にほぼ無関係です。一方、AL値も±15％程度の精度が得られており、表1の計算式が簡易的ではありますが磁気回路の設計に有効であることを裏付けています^＊4）。

参考
EER25.5の実測式　　AL＝79.745×lg^−0.7453　NI＝196.7×lg^0.796
EI35　　の実測式　　AL＝213.73×lg^−0.6558　NI＝165.9×lg^0.707
EER35Zの実測式　　 AL＝169.52×lg^−0.708　 NI＝214.8×lg^0.7345

表2：コアのAL、NIの計算と実測の比較（Bms＝0.35T）

項目	PC47 EER25.5　lg＝0.3mm		PC47 EI35　lg＝0.3mm		PC47 EER35Z　lg＝0.3mm
		計算値	実測式	計算値	実測式	計算値	実測式
Ae（m2）	44.8×10−6		101×10−6		107×10−6
AL（nH/T2）	187.7	195.6	423	471	448	397
N･Isat（AT）	83.5	75.4	83.5	70.9	83.5	88.7
出典：TDK カタログ　20141203 ／ ferrite_mz_sw_e_ja.fm

＊4）近似式の誤差
　ギャップ長lgの狭い領域では、lg＋（l/μ_S）≈lg が成立しなくなります。例えば l＝90.8mm、μ_S＝3000では l/μ_S＝0.03mmですから実測0.1mmの値は近似式の0.13mmに相当します。したがって、
AL値は 近似値＞実測値 、NIsat値は 近似値＜実測値 となります。

　一方、ギャップ長が広い領域の誤差の原因の詳細は不明ですが、実測ではギャップ断面部のみならずギャップ部近傍からも空間に磁束が飛び出し、実質的にギャップ長が短くなる効果も一因です。

　次回はこれらの関係式を使って実際のトランスやチョークの設計について考えます。

執筆者プロフィール

加藤　博二（かとう　ひろじ）

1951年生まれ。1972年に松下電器産業（現パナソニック）に入社し、電子部品の市場品質担当を経た後、電源装置の開発・設計業務を担当。1979年からSPICEを独力で習得し、後日その経験を生かして、SPICE、有限要素法、熱流体解析ツールなどの数値解析ツールを活用した電源装置の設計手法の開発・導入に従事した。現在は、CAEコンサルタントSifoenのプロジェクト代表として、NPO法人「CAE懇話会」の解析塾のSPICEコースを担当するとともに、Webサイト「Sifoen」において、在職中の経験を基に、電子部品の構造とその使用方法、SPICE用モデルのモデリング手法、電源装置の設計手法、熱設計入門、有限要素法のキーポイントなどを、“分かって設計する”シリーズとして公開している。

⇒連載『中堅技術者に贈る電子部品“徹底”活用講座』バックナンバー