ジャンクション温度の計算(5)―― 繰り返しパルス列の温度計算:中堅技術者に贈る電子部品“徹底”活用講座(79)(2/2 ページ)
計算精度の検証
確認のため実際に8式をδ=0.2について計算してみると表1のようになります。ここでδ=0.2ですからパルス幅twで正規化されたパルス周期tsはts=tw/δ=5となります。また定常温度上昇ΔT1はΔT1=0.2×Rth(J-C)で定常温度になっています(計算点①)。
このような計算をδ=0.1〜0.5、それぞれ10パルスについて計算したものが表2です。また図3は表2をグラフ化したものでn=10の値に対する相対誤差で表示してあります。図から多くのハンドブックが採用しているパルス2個分(計算点③)では+10%程度の誤差持っていることが分かります。ただし誤差は高めに出るので得られた値は破壊に対しては安全側になります。
ですが+5%程度の誤差に抑える必要がある場合にはn=3(4パルス分)程度は計算する必要があると言えます(δ=0.5以下)。
一方、表2や図3から損失の時間比率δが小さいほど少ない計算回数で精度は高くなることが分かります。
したがってスイッチング電源のMOSFETの温度計算のように損失時比率δが1%以下である場合には1サイクル(2パルス)の計算で1.6%程度の誤差に収まります。このような背景から次回説明するようにスイッチング電源の温度計算ではn=1(2パルス)の値で求めることが広く行われています。
ただし図3や表2は繰り返しパルス列のみによる温度上昇分です。実際の温度上昇は定常(DC的)成分との合算値の12式で計算します。
表計算ソフトの近似曲線機能を使って表2のn=10のΔTについてδによる近似式を求めたものが11式です。また等価熱抵抗Rth(δ)は12式で計算することになります。
*:単パルス時の過渡熱抵抗
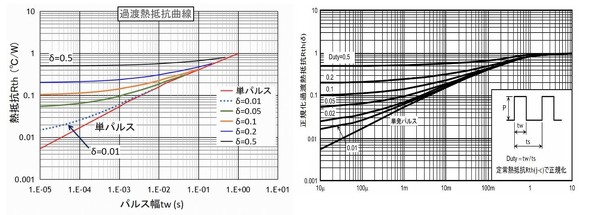
例えば1msの時の図1(a)の特性の正規化熱抵抗はRth(tw)=0.0532 Rth(J-C)=1.0ですから
▶δ=0.1の時
Rth(0.1)=0.1+0.781×0.0532=0.142
▶δ=0.2の時
Rth(0.2)=0.2+0.673×0.0532=0.236
▶δ=0.5の時
Rth(0.5)=0.5+0.4073×0.0532=0.522
図1(a)での読み値はそれぞれ0.14、0.24、0.52と読めますから十分な精度です。
この様子をδ=0.5まで求めた結果を図4に示しますが図1(a)の曲線と良好な一致を見せています。
ただし、本稿で考えている各式の前提条件は単パルスの過渡熱抵抗Rth(tw)が時間tの平方根(√t)に比例するとしています。
ですから図4の例では30msを超えるとこの前提条件から外れてきます。例えばδ=0.01ではtwは
tw=ts×δですから30ms×0.01=300μs以上では計算に誤差が含まれるようになり、n=3、すなわち10ms程度が計算式の限界になります。
したがってここで仮定した前提条件から外れる長時間域ではRth(tw)をグラフから読み取って繰り返し計算を愚直に行う必要があります。
また、ここではδ≦0.5以下についてグラフ化しましたが0.5を越える場合は記載していません。実際の温度計算でもそのようなケースはほとんどなく、それ故か多くのハンドブックでもδ=0.5程度が上限となっています。
今回は繰り返しパルス列の温度上昇について説明をしてきました。パルス損失が問題になる実際のスイッチング電源ではスイッチング周期に占める損失発生時間比率(δ)が極めて小さいことが分かっていますので1回の繰り返し、つまり2発のパルスによる温度変化を調べれば十分だと分かります。
次回は実際の損失波形を取り上げて温度計算を行い理論の精度を考えます。
執筆者プロフィール
加藤 博二(かとう ひろじ)
1951年生まれ。1972年に松下電器産業(現パナソニック)に入社し、電子部品の市場品質担当を経た後、電源装置の開発・設計業務を担当。1979年からSPICEを独力で習得し、後日その経験を生かして、SPICE、有限要素法、熱流体解析ツールなどの数値解析ツールを活用した電源装置の設計手法の開発・導入に従事した。現在は、CAEコンサルタントSifoenのプロジェクト代表として、NPO法人「CAE懇話会」の解析塾のSPICEコースを担当するとともに、Webサイト「Sifoen」において、在職中の経験を基に、電子部品の構造とその使用方法、SPICE用モデルのモデリング手法、電源装置の設計手法、熱設計入門、有限要素法のキーポイントなどを、“分かって設計する”シリーズとして公開している。
関連記事
 ワイヤーボンド(4) ―― 銅ワイヤーの評価項目とその注意点
ワイヤーボンド(4) ―― 銅ワイヤーの評価項目とその注意点
今回はコストダウンの一環として導入が進められている銅ワイヤーの評価項目とその注意点について説明します。 ワイヤーボンド(3) ―― ワイヤーボンドの評価法
ワイヤーボンド(3) ―― ワイヤーボンドの評価法
今回は銅ワイヤーについて説明する予定でしたが、その一環としてワイヤーボンドの評価法について説明します。 ワイヤーボンド(2) ―― 関連用語や治具、不良について
ワイヤーボンド(2) ―― 関連用語や治具、不良について
今回はワイヤーボンドの用語、治具および、ワイヤーボンドの不良について説明します。 ワイヤーボンド(1) ―― ワイヤーボンディングとは
ワイヤーボンド(1) ―― ワイヤーボンディングとは
今回から、半導体チップと外部電極との接続する「ワイヤーボンド」について解説していきます。 半導体(7) ―― MOSFETのゲート駆動回路の注意点(2)
半導体(7) ―― MOSFETのゲート駆動回路の注意点(2)
今回はパワーMOSFETの構造とそれに起因する寄生容量について説明するとともに、引き続きゲート駆動回路を中心にした使い方の注意事項を説明します。前回の記事と併せて読んでいただければ理解も深まると思います。 半導体(1) ―― 半導体の製造工程
半導体(1) ―― 半導体の製造工程
今回からは電子回路に欠かせない半導体について説明します。本シリーズでは半導体の市場不良および、その原因を説明するための製造工程の問題を主眼に説明をしていきます。
Copyright © ITmedia, Inc. All Rights Reserved.
記事ランキング
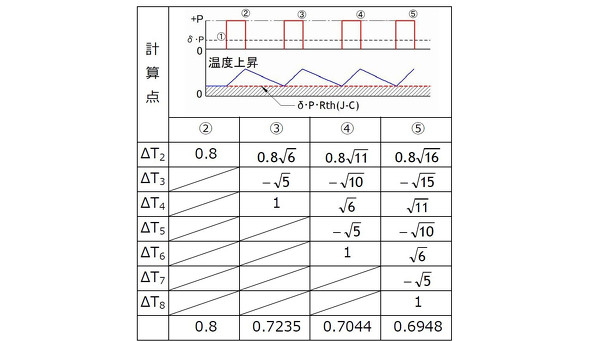 表1:δ=0.2の計算結果
表1:δ=0.2の計算結果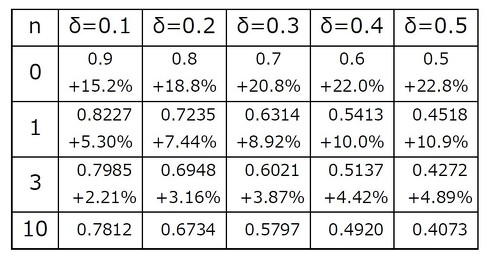 表2:繰り返しパルス列の温度上昇(ΔT)の収束
表2:繰り返しパルス列の温度上昇(ΔT)の収束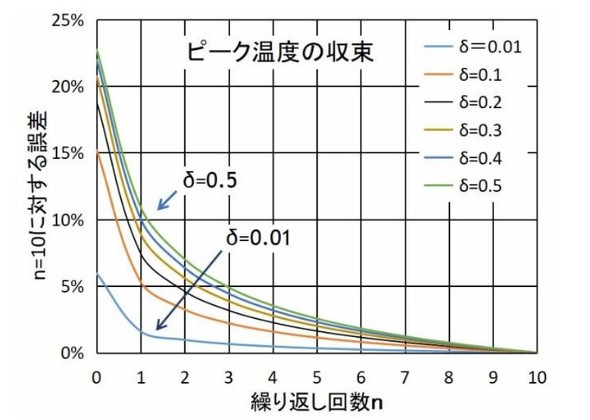 図3:繰り返しパルスのピーク温度の収束
図3:繰り返しパルスのピーク温度の収束