ジャンクション温度の計算（6）―― 実機のスイッチング素子の温度計算：中堅技術者に贈る電子部品“徹底”活用講座（最終回）（4/4 ページ）

[加藤博二（Sifoen），EDN Japan]

熱抵抗が√(t)に当てはまらない場合

　ここまでは全て過渡熱抵抗Rth(t)が√(t)に比例するものとして説明、計算してきました。

　この項ではこの条件から外れてパルスの印加時間が長くなり過渡熱抵抗の屈曲点（図6（a）赤丸部）をまたぐ時間域の温度上昇を考えます。
　このような事例は前述したキャパシタ回路への充電（突入）電流波形などが該当し、波形の多くは過渡熱抵抗の屈曲点をまたぐ数ms〜数十msの時間域となります。

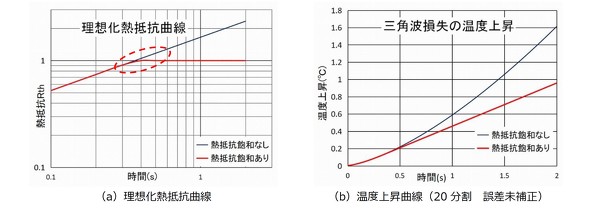
　図6（a）は過渡熱抵抗の飽和（Rth_(J-C)による制限）の有無を2直線で理想化したものです。ここでは温度上昇の計算例として図6（a）の屈曲点（赤丸部　t＝0.365s）をまたぐパルス幅2s、ピーク1Wの⊿形の損失を与えた場合の温度上昇を考えます。

　計算手法として損失波形を20分割して計算を実行し、過渡熱抵抗の飽和の有無の差を検証します。
　なお過渡熱抵抗RthはRth(t)＝1.655×√(t)で規定されるものとします。

1. 最初に屈曲点がなく、熱抵抗が際限なく√(t)に比例する場合は1.61℃の温度上昇となりました。20分割した場合の誤差（＋3.42％）は＋方向ですので得られた値から推定した値は1.61/1.03＝1.56℃です。
   この手法の検証のため理論値を考えます。このケース（損失が⊿形）の場合には従来の温度上昇の理論式が使えます。過渡熱抵抗Rthは
   　　Rth＝1.655×√(t)
   ですのでΔT＝2/3×Rth(2)＝0.666×1.655×1.414＝1.56℃となり計算手法に問題がないことを確認できました。図6（b）の曲線はこの誤差の補正を行っていない20分割の場合の曲線です。
2. 過渡熱抵抗が制限される場合
   t＞0.365sで過渡熱抵抗は飽和しますので今まで用いてきた理論式は使えません。ですから温度計算には波形を分割してそれぞれの損失と印加時間に応じた温度上昇を計算し、時間ごとの総和を得る必要があります。
   図6（b）はその考え方で波形を20分割し、各時間幅の熱抵抗を算出して計算したものです。
   過渡熱抵抗Rth(t)がRth_(J-C)に漸近する場合には温度上昇は0.96℃となって「1. 」の場合に対して低く出ることが分かります。これは図6（a）から分かるように0.365sを超えると長時間の過渡熱抵抗が時間とともに増加しないことに起因します。
   　実際には屈曲点を超えたからといって即、温度が一定になるのではなく、計算に使用した各時間の過渡熱抵抗Rth(t)の多くがRth_(J-C)に入れ替わって初めて温度に影響が出てきます。図6から
   　　5％程度の誤差を許容するのであれば屈曲時間×1.4倍程度
   　　10％程度の誤差を許容するのであれば屈曲時間×1.6倍程度
   の時間までは理論式が使用できることが分かります。

図6：過渡熱抵抗が√(t)から外れる場合［クリックで拡大］

　ここでは2直線化した例を検証しましたが実際にはチップ〜ダイボンド〜フレーム〜パッケージ〜サーマルグリース〜放熱器と熱が伝わり、その都度熱抵抗の様子（傾き）が変わります。
　ですから実際の温度計算を行う場合は、損失波形の瞬時データと熱抵抗から重ね合わせの理を使って温度を求めることになります。
　瞬時損失波形を得るにはデジタルオシロスコープの電圧、電流波形のCSVデータを使用して計算するか、あるいは画像読み取りソフトウェアを使用して絵としての電圧、電流波形をCSVデータ化します。

---

本連載を振り返って

　2016年10月31日のフェライトから始まった本連載も今回で最終回となります。
　もともと本シリーズは「フェライトは酸化鉄の焼結体……」 、 「湿式電解コンデンサは電解液が誘電体……」 、 「4級塩電解液は強アルカリ……」 、 「銅ワイヤーボンディングは金ワイヤーと同品質……」 など、誤った情報の訂正も兼ねて背景になる技術の説明を通じて正しい部品の使い方を説明する目的で始まったものです。
　そのような観点からプリント基板やはんだ付け、電子部品の取り扱い、保管、洗浄などは固有の注意が必要なのですがディレーティングや禁止事項とは直接結び付かないために積み残しになりました。これらの話は別途、何かの機会に紹介したいと思います。

　また本シリーズで取り上げた銅ワイヤーボンディングについてはボンディング材としての銅の材料特性の疑問を解消しないまま2010年代の当初に『銅ワイヤーに品質問題はない。銅ワイヤーに起因する品質問題については全て当社の責任で対応する』と署名、押印した推進派の半導体メーカーも存在しました。しかしそのメーカー自身が2016年発足のAECの銅ワイヤー問題小委員会に名前を連ねていますので機会があれば臨席姿勢を聞いてみたいものです。

謝辞
　最後になりますが読者の皆さま、そして私の文章を丁寧に編集し、より良い形に仕上げてくださった編集の皆さまに深く感謝の意を表します。私も7年間にわたる連載を通じて経験や知識を整理し補填することができ、本当にありがとうございました。
　また超初心者を対象にした新しい連載も予定していますので、どうぞ引き続きご支援いただけますようお願い申し上げます。

---

執筆者プロフィール

加藤　博二（かとう　ひろじ）

1951年生まれ。1972年に松下電器産業（現パナソニック）に入社し、電子部品の市場品質担当を経た後、電源装置の開発・設計業務を担当。1979年からSPICEを独力で習得し、後日その経験を生かして、SPICE、有限要素法、熱流体解析ツールなどの数値解析ツールを活用した電源装置の設計手法の開発・導入に従事した。現在は、CAEコンサルタントSifoenのプロジェクト代表として、NPO法人「CAE懇話会」の解析塾のSPICEコースを担当するとともに、Webサイト「Sifoen」において、在職中の経験を基に、電子部品の構造とその使用方法、SPICE用モデルのモデリング手法、電源装置の設計手法、熱設計入門、有限要素法のキーポイントなどを、“分かって設計する”シリーズとして公開している。

⇒連載『中堅技術者に贈る電子部品“徹底”活用講座』バックナンバー